分治策略

在上一篇笔记中,我们提到了一种算法设计策略:归并排序,当时没有深入展开,而本章会就这个算法策略展开一系列的分析和说明。

所谓分治策略,其基本思想就是将原问题递归地划分为一系列的子问题,不停地减小问题的规模,直到能够轻易解决,然后将各个子问题的解合并起来,还原为原来问题的解。简单来说就是分而治之！

其具体的递归步骤主要有以下三步:

• 分解(Divide): 将问题划分为一些子问题,子问题的形式与原问题一样,只是规模更小.
• 解决(Conquer): 递归地求解出子问题。如果子问题的规模足够小,则停止递归,直接求解.
• 合并(Combine): 将子问题的解组合成原问题的解.

但是,需要注意的是并不是所有可以递归分解的问题都是可以用分治策略来解决的,其中关键的一点是在递归过程中是否存在overlap,如果存在的话,那就不应该使用分治策略,在这种情况下,分治的结果会很差,此时我们可以使用另外一种算法策略来解决问题:动态规划.关于什么是overlap和动态规划,书中的后续章节都会有所涉及,这里只是过一个简单的提醒——分治策略不是万能的。

分治算法举例

书中一共有三个使用了分治策略的算法,分别是归并排序,最大子数组以及Strassen算法,其中的Strassen算法比较罗嗦,这里就不举例了,大家可以去看书中的论述。

归并排序

这可以说是最基本的一个排序算法了,任何一个学习过编程的人都应该知道这个算法,这里为了完整性,简要说明一下。

归并算法:

1. 分解待排序的\(n\)个元素的序列成各自具有\(\frac{n}{2}\)个元素的两个子序列。(Divide)

2. 使用归并排序递归地排序这两个子序列。(Conquer)

3. 合并两个已经排好序的子序列。(Combine)

Python实现如下:

#!python
def merge_sort(A):
    if len(A) == 1:
        return A
    else:
        mid = len(A) // 2
        left = merge_sort(A[:mid])
        right = merge_sort(A[mid:])
        result = merge(left,right)
    return result

def merge(left,right):
    i = 0
    j = 0
    result = []
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    else:
        if i < len(left):
            result += left[i:]
        if j < len(right):
            result += right[j:]
    return result

if __name__ == "__main__":
    #A = [1,3,4,5,1,2,3,20,2,345]
    A = [12,100,230,1,3,4,5,1,2,3,20,2,345]
    print(A)
    B = merge_sort(A)
    print(B)

最大子数组

问题描述:给定一个元素值有正有负的数组,从中找出一个子数组,使得其和在所有可能的情况中最大。

• Input: \([13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]\)
• Output: \([18,20,-7,12]\)

因为在所有的子数组中的,\(18+20+(-7)+12=43\)是最大的。

对于这个问题,我们同样可以使用分治策略来解决。如果我们将长度为\(n\)数组\(C\)以其中点为分界点,分解成两个长度为\(\frac{n}{2}\)的子数组\(A\)和\(B\),那么最大子数组\(K\)必然存在于下面三种情况之一:

1. \(K\)存在于\(A\)中
2. \(K\)存在于\(B\)中
3. \(K\)包含\(C\)的中点,也即\(K\)横跨\(A\)和\(B\)

在这三种情况中,前两种很容易处理,只需要不断递归下去,直到终止状态,而对于第三种情况,我们需要在进行合并的时候,从中点开始向两边扩展,寻找可能的\(K\),并将找到的结果和\(A,B\)中找到的\(K\)作比较,取其最大者。

需要注意的是,这里可以从中间往两边扩展进行寻找,因为在这个问题上加法具有这样的性质:两个较大的数的和也会是一个比较"大"的数,而这种性质是不适用于乘法的¹.如果是正数和负数相乘,那就只能得到一个更小的数。

终止条件: 不断的向下递归,直到数组中是剩下一个元素,返回该数组。

Python实现如下所示:

#!python

def merge_maxsubsum(array,start=None,end=None):
    if start == None:
        start = 0
    if end == None:
        end = len(array) - 1
    if end >= len(array):
        raise Exception("The end is larger than the length!")
    if start == end:
        return (start,end,array[start])
    else:
        mid = (start + end ) // 2
        left  = merge_maxsubsum(array,start,mid)
        right = merge_maxsubsum(array,mid+1,end)
        across = merge_across(array,start,mid,end)
        return max([left,right,across],key=lambda x:x[-1])

def merge_across(array,start,mid,end):
    left_sum = mid
    left_max_sum = float("-inf")
    for i in range(mid,start-1,-1):
        left_sum += array[i]
        if left_sum > left_max_sum:
            left_max_sum = left_sum
            left_start = i
    right_sum = mid
    right_max_sum = float("-inf")
    for i in range(mid+1,end+1):
        right_sum += array[i]
        if right_sum > right_max_sum:
            right_max_sum = right_sum
            right_end = i
    return (left_start,right_end,left_max_sum + right_max_sum)

递归式的分析

书中一个讲解了三种解决递归式的方法,分别是:代入法,递归树和主方法.接下来会主要介绍这三种不同的方式

代入法

这其实是一种"瞎猜"的方式,基本思想就是猜出一个解,然后用数学归纳法验证。其主要步骤如下所示:

1. 猜测解的形式
2. 用数学归纳法求出解中的常数,并证明解是正确的。

代入法主要依靠的是人的经验和直觉,如果看到一个递归式能快速地反应出其解的形式,者无疑是最好的,但是这需要大量的练习才能做到。

递归树

这种方式就比较简单了,就是按照其递归过程,将原问题画成一棵递归树,从递归树中计算出解的形式. 比如归并排序的递归式\(T(N)=2f(\frac{N}{2})+N\)的递归树就是:

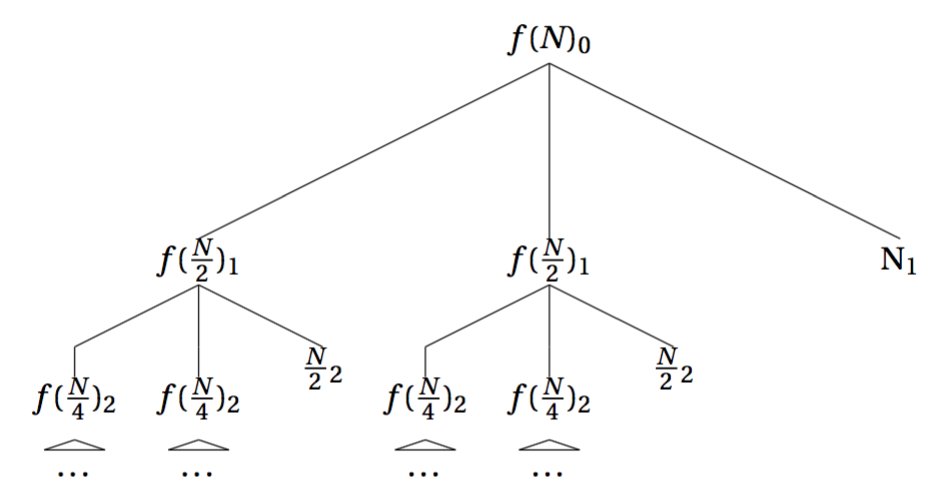
其中,每个节点上的下标数字表示的当前节点所处的层数。

分析工具

在进行递归树分析的时候,我们需要用到一些数学工具来辅助我们,这里列出几个我们后续计算中需要用到的工具。

1. 递归树的深度

假设某一棵递归树的递归过程是\( N\rightarrow\frac{N}{c}\rightarrow\frac{N}{c^2}\dots\),则其深度\(m\)则应该满足:

1. 几何级数求和

几何级数的求和公式为\(S=1+x+x^2 + x^3 + \cdots + x^k=\frac{x^{k+1}-1}{x-1}\).

• 当\(x=1\)时, \(S=k+1\)
• 当\(x<1\)时, \(S=O(1)\)
• 当\(x>1\)时, \(S=x^k (1+\frac{1}{x}+\frac{1}{x^2}\cdots) = O(x^k)\)

分析举例

这里依然用归并排序的例子举例,归并排序的递归式是\(T(N)=2T(\frac{N}{2})+N\),其递归树上面已经给出。现在我们需要根据这个递归树,计算出归并排序的真正时间复杂度。

在计算递归树的时候,我们首先计算两个关键的值:

1. 递归树一共有多少层
2. 每一层的计算代价是什么

对于第一个问题,很简单,这个递归树的层数是\(\log_2 N\)。

现在考虑第二个问题,很显然,第一层的代价是\(N\),第二层的代价是\(2 \times \frac{N}{2}=N\),第三层的代价是\(4\times \frac{N}{4}=N\), 则第\(k\)层的代价是\(2^{k-1} \times \frac{N}{2^{k-1}} =N\),因此所有层的代价之和为\(\sum\limits_{i=1}^{\log_2 N} N\).

注意，这还不是最后答案，我们还需要考虑递归树的叶子节点，当递归树到达叶节点时，一共有\(2^{\log_2 N} = N\)个\(f(1)\)，因此在基础情况下的代价是\(N \times f(1)\)。而我们认为\(f(1)=O(1)\)，所以叶节点的代价就是\(O(N)\).

所以整个递归树的代价就是\(O(\sum\limits_{i=1}^{\log_2 N} N) + O(N)=O(N\log_2 N)\).

主方法

这种方式主要是用来解决形如\(T(n)=aT(\frac{n}{b})+f(n)\)的递归式,其中\(a\ge 1,b>1\)是常数,\(f(n)\)是渐进函数。

这个式子可以做如下的理解: 将规模为\(n\)的问题分解为\(a\)个子问题,其中每个子问题的规模为\(\frac{n}{b}\),而函数\(f(n)\)包含了问题分解和子问题合并的代价。

主方法主要由以下的定理构成:

主定理:

令\(a\ge 1,b>1\)是常数,\(f(n)\)是一个函数,\(T(n)\)是定义在非负整数上的递归式:

$$ T(n) = aT(\frac{n}{b}) + f(n) $$

那么\(T(n)\)有如下的渐进界:

1. 若对某个常数\(\epsilon > 0\)有\(f(n)=O(n^{\log_b^{a-\epsilon}})\),则\(T(n)=\Theta(n^{\log_b^a})\)

2. 若\(f(n)=\Theta(n^{\log_b^a})\),则\(T(n)=\Theta(n^{\log_b^a} \lg n)\)

3. 若对某个常数\(\epsilon > 0\),有\(f(n)=\Omega(n^{\log_b^{a+\epsilon}})\),且对某个常数\(c<1\)和所有足够大的\(n\)有\(af(\frac{n}{b})\le cf(n)\),则\(T(n)=\Theta(f(n))\)

参考资料

• 算法导论第四章
• Utah大学Aditya Bhaskara教授的Advanced Algorithm课程

修改日志

• 2014年8月5日 首次发布
• 2016年8月30日 增加递归树分析举例

Share on: Twitter ❄ Facebook ❄ Email

---

Comments

So what do you think? Did I miss something? Is any part unclear? Leave your comments below

Comments

comments powered by Disqus

---