写在前面

这篇笔记是直接跟在第四章的笔记之后，之所以跳过了第五章，主要是因为第五章的内容涉及到了随机算法的内容，而这部分内容我之前有另外一个系列的笔记，是专门记录随机算法学习过程的。其中涉及到的内容要比CLRS中的多很多，因此这一章我就直接跳过了，具体内容看参看我那一个系列的笔记。

堆

(二叉)堆是一种基本的数据结构，通常来说是用数组来实现的，它可以看成是一个完全二叉树，树中的每一个节点表示堆中的一个元素。如下图所示:

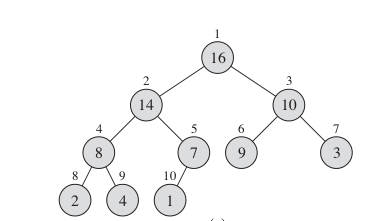
对于一个最大(最小)堆来说，最重要的性质是:树中的父节点永远不小(不大)于它的子节点.

另外，由于堆的实现是用数组来实现的，且又是一个二叉树，如果下标是从1开始的，那么它具有如下的性质:对于任意的节点i(当前节点的下标)，它的父节点是\(\lfloor \frac{i}{2}\rfloor\),而且左右孩子分别为\(i\times 2\)和\(i\times 2+1\).这个性质对于我们的实现来说，提供了比较大的帮助.

这里将会用最大堆来举例。

对于一个最大堆来说，它一共有如下的几个操作:

• MAX-HEAPIFY: 维护最大堆的性质
• BUILD-MAX-HEAP: 从无序的输入数组中构造一个最大堆
• HEAPSORT: 对一个数组进行堆排序

关于堆各种操作的伪代码CLRS上面都有，这里就不再重复了，直接给出堆的实现:

#!python
#!/usr/bin/python3
#coding:utf-8
"""
Program: 堆排序的实现
Description: 
Author: Flyaway - flyaway1217@gmail.com
Date: 2014-08-06 15:41:27
Last modified: 2014-08-08 15:21:15
Python release: 3.3.1
"""

class MyMaxHeap:

    def __init__(self,array):
        self._array = [float("-inf")]
        self._array[1:] = array
        self._heap_size = len(self._array) - 1
        self._build_max_heap()

    def _left(self,i):
        return i<<1

    def _right(self,i):
        return (i << 1) + 1

    def _parent(self,i):
        return i>>1

    def _max_heap(self,i):
        left = self._left(i)
        right = self._right(i)


        if left > self._heap_size :
            left = 0
        if right > self._heap_size:
            right = 0

        # find the largest 
        largest = max([left,right,i],key=lambda x: self._array[x])

        if largest == i:
            return
        else:
            (self._array[largest],self._array[i]) = (self._array[i],self._array[largest])
            self._max_heap(largest)

    def _build_max_heap(self):
        for i in range(self._heap_size//2,0,-1):
            self._max_heap(i)

    def __str__(self):
        s = ' '.join([ str(item) for item in self._array[1:] ])
        return s

    def __repr__(self):
        s = ' '.join([ str(item) for item in self._array[1:] ])
        return s


if __name__ == "__main__":
    array = [1,4,2,3,9,7,8,10,14,16]
    maxheap = MyMaxHeap(array)
    print(maxheap)

堆排序

而堆排序是建立在堆这个数据结构之上的，由于堆的结构性质保证了它的第一个元素一定是这个数据序列中最大的元素，因此将它与序列中的最后一个元素交换，则它就处于它排好序之后的位置上了。此时，将堆的size缩小一(将已经放置到末尾的最大元素去除)，然后重建堆结构。不断重复上述过程，直至堆结构中只剩下一个元素。在这个过程中，我们利用了堆的第一个元素一定是当前堆中最大元素这个性质。具体代码实现如下:

#!python
def heap_sort(self):
    for i in range(self._heap_size,0,-1):
        (self._array[i],self._array[1]) = (self._array[1],self._array[i])
        self._heap_size -= 1
        self._max_heap(1)

优先队列

堆这种数据结构还有一种比较重要的用途，那就是用来实现优先队列，优先队列在操作系统中有着非常重要的作用。

此处用最大优先队列来举例，一个最大优先队列有如下的操作:

• INSERT(S,x): 把元素\(x\)插入到集合\(S\)中。
• MAXIMUM(S): 返回\(S\)中具有最大关键字的元素。
• EXTRACT-MAX(S): 去掉并返回\(S\)中具有最大关键字的元素。
• INCREASE-KEY(S,x,k): 将元素\(x\)的关键字值增加到k。

具体代码如下所示:

#!python
#!/usr/bin/python3
#coding:utf-8
"""
Program: 最大优先队列的实现
Description: 
Author: Flyaway - flyaway1217@gmail.com
Date: 2014-08-12 15:19:05
Last modified: 2014-08-12 15:53:26
Python release: 3.3.1
"""

class MaxHeap:

    def __init__(self,array):
        self._array = [float("-inf")]
        self._array[1:] = array
        self._heap_size = len(self._array) - 1
        self._build_max_heap()


    def _left(self,i):
        return i<<1

    def _right(self,i):
        return (i << 1) + 1

    def _parent(self,i):
        return i>>1

    def _max_heap(self,i):
        """Ensure the property of max heap
        """
        left = self._left(i)
        right = self._right(i)


        if left > self._heap_size :
            left = 0
        if right > self._heap_size:
            right = 0

        # find the largest 
        largest = max([left,right,i],key=lambda x: self._array[x])

        if largest == i:
            return
        else:
            (self._array[largest],self._array[i]) = (self._array[i],self._array[largest])
            self._max_heap(largest)


    def _build_max_heap(self):
        for i in range(self._heap_size//2,0,-1):
            self._max_heap(i)

    def __str__(self):
        s = ' '.join([ str(item) for item in self._array[1:self._heap_size+1] ])
        return s

    def __repr__(self):
        s = ' '.join([ str(item) for item in self._array[1:self._heap_size+1] ])
        return s


    def maximum(self):
        '''Return the max item
        '''
        return self._array[1]

    def extract_max(self):
        """Return and move the max item
        """
        if self._heap_size < 1:
            raise Exception("Heap underflow")

        maximum = self._array[1]
        self._array[1] = self._array[-1]
        self._heap_size -= 1
        self._max_heap(1)
        return maximum

    def increase_key(self,i,k):
        """Increase the item specified by i to k.

        Arguments:
            i: the indicator of the item
            k: the value the item need to increased to

        Returns:
        """
        if i <= 0:
            raise Exception("the item does not exit!")

        if k < self._array[i]:
            raise Exception("new key is smaller than current key")

        self._array[i] = k

        parent = self._parent(i)
        while parent >= 1 and self._array[parent] < self._array[i]:
            self._array[parent],self._array[i] = self._array[i],self._array[parent]
            i = parent
            parent = self._parent(i)


    def insert(self,x):
        self._heap_size += 1
        if self._heap_size >= len(self._array):
            self._array.append(float("-inf"))
        else:
            self._array[self._heap_size] = float("-inf")
        self.increase_key(self._heap_size,x)


if __name__ == "__main__":
    data = [15,13,9,5,12,8,7,4,0,6,2,1]
    maxheap = MaxHeap(data)

    print("The original max heap:")
    print(maxheap)
    print("-"*50)

    print("After extract_max():")
    print(maxheap.extract_max())
    print(maxheap)
    print("-"*50)

    print("After maximum():")
    print(maxheap.maximum())
    print(maxheap)
    print("-"*50)


    print("After increase_key(2,20):")
    maxheap.increase_key(2,20)
    print(maxheap)
    print("-"*50)

    print("After insert(40):")
    maxheap.insert(40)
    print(maxheap)
    print("-"*50)

    print("After insert(12):")
    maxheap.insert(12)
    print(maxheap)
    print("-"*50)

Share on: Twitter ❄ Facebook ❄ Email

---

Comments

So what do you think? Did I miss something? Is any part unclear? Leave your comments below

Comments

comments powered by Disqus

---