本章的核心问题是给定一个长度为\(n\)的乱序序列，从中找出第\(k\)小的元素.如果把这个问题特例化，令\(k=\lceil n/2 \rceil\)那就是寻找中位数。其实，最基本的想法就是先对序列进行排序,然后在排好序的结果中取出第\(k\)个元素。这不失为一种比较好的方法，但是需要知道的是，排序算法的下界是\(O(n\log n)\)，而在很多情况下，我们希望能够得到更好的算法，本章就是讨论怎样在线性时间内解决这个问题的。

随机化算法

CLRS上的这一部分内容个人觉得写得并不好，不容易被人理解，虽然我原来就了解了这个算法的整个过程和证明，但是看CLRS还是觉得无法理解清楚。之前我写过另外一篇博文，专门用来说明如何使用随机算法来寻找中位数，整个过程其实是比较复杂，具体可以参看这篇文章 中的问题举例一节。

确定性算法

个人觉得确定性算法的证明部分CLRS论述的不是很好，感觉有点由结果推原因，因此我重新整理了一下思路¹，重新说明一下。

首先来说明算法步骤:

Select算法:

input: 一个包含了\(n\)个数的集合\(A\)和一个整数\(k\), \(1\le k \le n\)

outpout: 元素\(x\in A\)，且\(A\)中恰好有\(k-1\)个其他元素小于\(x\)

1. 将输入数组的\(n\)个元素划分为\(\lceil \frac{n}{5} \rceil\)组，每组有5个元素(最后一组除外，最后一组应该小于等于5个元素). \(O(n)\)
2. 寻找这\(\lceil \frac{n}{5} \rceil\)组中每一组的中位数,对每组中的5个元素进行排序，然后取出中位数。\(O(n)\)
3. 对于第2步中找到的\(\lceil \frac{n}{5} \rceil\)个中位数，递归调用Select算法以找到其中位数x.
4. 将原来的数组\(A\)重新按照中位数的中位数\(x\)进行划分，所有小于等于\(x\)的元素都放在\(x\)的左侧，所有大于\(x\)的元素都放在\(x\)的右侧。令\(i\)表示此时\(x\)所处在下标位置。\(O(n)\)
5. 如果\(i==k\),则返回\(x\).如果\(i < k\)，则在\(x\)右侧的高区递归查找第\(k-i\)小的元素；如果\( i > k $，则在\)x\(左侧的低区递归查找第\)k$小的元素。

每一个步骤需要花费的代价，我都在每一个步骤的最后标出来了，其中3、5步骤由于涉及到递归过程，需要额外分析。

首先，令\(T(n)\)表示Select算法的最坏运行时间，那么第3步中花费的代价就是\(T(\lceil \frac{n}{5} \rceil)\)，需要进一步分析的是第5步，我们需要分析，在第五步中最坏情况下有多少元素会被砍掉。

这可以从下图中看出：

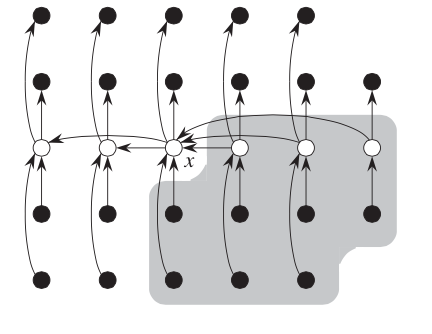
阴影部分就是可以确定大于\(x\)的元素，可以看到，除了\(x\)自己所在的组和最后一个不满5个元素的那组外，至少有一半的分组中有3个元素大于\(x\)，因此大于\(x\)的元素个数\(N_{>x}\)至少是:

同理，小于\(x\)的元素至少为\(N_{<x}\ge\frac{3n}{10} - 6\).

因此，每一次做第5步的时候，我们都会砍掉\(\frac{3n}{10} - 6\)个元素，也即最多会有\(\frac{7n}{10} + 6\)个元素会进入下一轮的递归,所以第5步的代价是\(T(\frac{7n}{10} + 6)\)

因此，我们可以列出递归式:

现在我们就需要证明这个\(T(n)\)是线性的, 即证明，存在正常数\(c\)和\(n_0\),使得\(n\ge 0\)，有\(T(n)\le cn\),这可以通过替换法来完成。

假设\(T(n)\)是线性的，则当\(n\ge n_0\)时，\(T(n)\le cn\),同时，每一轮算法中还需要花费\(O(n)\)，因此我们还需要引入一个常量\(a\)，用\(an\)来表示\(O(n)\)的上界。代入到递归式的右边，我们可以得到:

如果\(T(n)\)确实是线性的，那么:

因此，我们可以取\(n_0 > 70 $,此时\)c \ge \frac{-10an}{70-n} > 0\(，因此当\)n>n_0=70\(时，存在正常数\)c\(使得\)T(n)<cn\(,因此，\)T(n)$是线性的。

代码实现

#!python
# !/usr/bin/env python3
# -*- coding:utf-8 -*-
#
# Author: Flyaway - flyaway1217@gmail.com
# Blog: zhouyichu.com
#
# Python release: 3.4.1
#
# Date: 2014-12-16 10:46:11
# Last modified: 2014-12-17 11:27:15

"""
The implement of the Select algorithm which find the kth small item from an unsorted array.
"""


def partition(arg_array,x):
    array = arg_array[:]

    index = array.index(x)
    array[-1],array[index]  = array[index],array[-1]

    i = -1
    for j in range(len(array)-1):
        if array[j] < x:
            i += 1
            array[i],array[j]  = array[j],array[i] 
    array[-1],array[i+1]  = array[i+1],array[-1] 
    return array


def Select(arg_array,k):

    array = arg_array[:]

    # boundary condition
    if len(array) == 1:
        return array[0]

    # 1. Split the groups 
    i = 0
    groups = []
    while i+5 < len(array):
        groups.append(array[i:i+5])
        i += 5
    groups.append(array[i:])

    #2. Sort each group
    newarray= []
    for group in groups:
        newarray.append(sorted(group)[len(group)//2])

    #3. find the middle of the middle number
    x = Select(newarray,len(newarray)//2)

    #4. Partition
    array = partition(array,x)
    index = array.index(x)

    #print(array,end="\t")
    #print("k=" + str(k),end="\t")
    #print("x=" + str(x), end ="\t")
    #print("index=" + str(index))

    # 5.Recursion
    if index == k:
        return x
    elif index > k:
        return Select(array[:index],k)
    else:
        return Select(array[index+1:],k - index - 1)


if __name__ == "__main__":

    #array = [4,5,6,-1,10,1,2,3]
    array = [5,6,102,10,8,9,-109,4,10,5,6,-3,10,7,2,-5,3,1,0]
    #print(partition(array,5))
    for i in range(len(array)):
        x = Select(array,i)
        print(x == sorted(array)[i])

    #print(Select(array,5))
    #print(sorted(array)[5])

Share on: Twitter ❄ Facebook ❄ Email