前言
最近在看斯坦福的《机器学习》的公开课,这个课程是2009年的,有点老了,不过讲的还是很好的,廓清了一些我以前关于机器学习懵懂的地方。我的一位老师曾经说过:
什么叫理解?理解就是你能把同一个事情用自己的语言表达出来,并且能让别人听得懂。
本着这样的原则,同时也为了证明自己是"理解"的,于是决定打算在学习《机器学习》公开课的时候,写一些系列文章类巩固学到的东西。机器学习中的很多内容都是和数学推导相关的,而我本人的数学功底并不扎实,所以文章也许会写得比较慢。另外,这个系列的文章大体上是按照公开课的课程来的,但也不一定局限于它,因为同时手头还有很多其他的学习资料,学到哪里就写到哪里吧,但我也会尽量保持连贯性1。
这篇文章的关注点在于 线性回归问题,重点是求解线性回归问题的梯度下降法(Gradient Descent),之前在学习感知机的时候,使用过这个算法,并且还在这里了它。可是那只是仅仅停留在使用的层面上,这次是要充分理解梯度下降法的原理及其计算方法。
线性回归问题
从数学上说, 回归问题其实就是函数拟合问题:给定一些点的集合,然后用一个曲线2或方程去拟合,使得集合中的所有点都大致符合给出的曲线或方程。当拟合的曲线是一条直线的时候,就称为是线性回归问题。
回归问题的意义在于,它使得我们能够在已知数据的基础上对未知数据进行预测:通过对已知数据进行回归分析,得到一个曲线,我们就能够利用这个曲线对未知的数据进行很好的预测。其实,我们在初高中就遇到过这种问题了,只是我们当时被没有意识到这是一个回归问题。
例如给定两个点\((x_1,y_1)\),\((x_2,y_2)\),求过这两个点的直线。当然,现在我们的问题复杂得多,而且不仅仅局限在二维平面,很多时候都是处理高维数据。
举了例子3,现在我们有如下的数据:
| Living area | bedrooms | Price |
|---|---|---|
| 2104 | 3 | 400 |
| 1600 | 3 | 330 |
| 2400 | 3 | 369 |
| 1416 | 2 | 232 |
| 3000 | 4 | 540 |
现在的问题是,我给定一个组新的Living area 和 bedrooms数据,你能否预测正确的Price是多少?这里的数据是三维的,但是更多时候是多维的,影响房价的因素还包括很多,如有浴室的数目、有没有壁炉等。这里的输入是Living area和beadrooms,输出则是Price。
在统计机器学习4中,影响输出的因素被称为是特征(features),输入数据称为训练集(training set)或训练数据(training data),训练数据的维度称为特征的个数。
因为我们的重点是线性回归问题,所以这里我们简单地假设能够拟合的方程是:
这里\(\theta_i\)称为参数(也称作是权重),这里的变量是\(x_1\)和\(x_2\),在我们的例子中分别代表Living area和bedrooms,\(h_\theta(x)\)是输出值,这里是就是Price。现在任务很明确,就是根据已知的数据计算出相应的\(\theta_i\)参数。整个过程可以用下图表示:
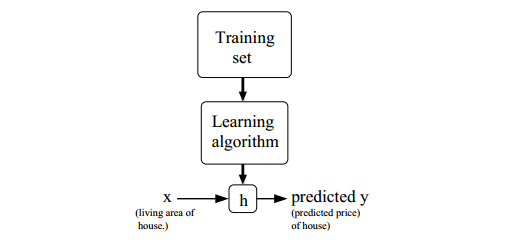
上图是整个统计机器学习的流程,不仅仅局限于回归问题。
为了一般化我们的公式,可以引入一个常量\(x_0=1\),这样我们的公式就可以表示为:
注意,这里有几个贯穿全文的约定:
- \(n\)代表的是特征的个数,也就是输入数据的维度
- \(m\)代表的是训练数据的数目
- \(x^{(i)}\)代表第i个训练数据
- \(x_{i}\)代表第i个特征
- 因为后面有很多公式都是向量的或矩阵的运算,为了区别开来,我会在所有表示向量或矩阵的变量的下标中注明维度。如果没有下表,则表示一个实数5。
现在我们已经有了一个假设的函数了,那么我们该如何衡量这个函数的好坏呢?这就要引入损失函数(cost function),这个函数用来衡量我们的预测值和真实值之间的差距。它是这样定义的:
这个函数很好理解,它是关于参数\(\theta_{n\times 1}\)的函数,直观上就是(预测值-真实值)的平方,然后对每一组训练数据进行累加,用这个累加和来衡量我们学习到的函数\(\eqref{origin}\)。这里的\(\frac{1}{2}\)其实并不是必须的,只是为了简化后面的推导而人为的乘上一个系数,这对结果不影响。如果搞过数模的话,就知道,这其实就是最小二乘法的思想。
梯度下降法
现在我们的问题就转化为一个求最小值的问题了:
如何求解这个问题呢?这里我们就要引入最小梯度法了。还记得当年学高数,在学到梯度的时候,记得老师曾经说过,负梯度方向是函数下降最快的方向。最小梯度法就是利用这个性质。具体的思路是:
- 对\(\theta_{n\times 1}\)进行赋值,这个值可以是随机的,但通常都赋值为一个全零的向量。
- 不停迭代,每次迭代都改变\(\theta_{n\times 1}\),使得\(J(\theta_{n\times 1})\)按梯度下降的方向进行减少。
上面的比较数学化的说法,其实比较直观的说法是这样的:想象你站在一座高山上,你想要用最短的时间下山,但是你每次只能走一步。那你需要做的就是查看你周围360度的范围,找到一个最陡峭的(下降的最快的)方向,然后转移到那个点上;转移到新的位置之后,重复相应的步骤,环顾360度,找到最陡峭的(下降的最快的)方向,然后转移过去,这样每次都是选择最陡峭的方向走,那么很快就能到达山下了。
这就是梯度下降法的基本思路,其中对陡峭的方向就是负梯度的方向。
为了更加易于理解,给出下图:
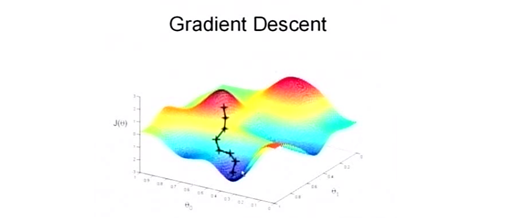
我们\(\theta_{n\times 1}\)按照梯度下降的方向进行调整,就会使得\(J(\theta_{n\times 1})\)往更低的方向进行变化,如上图所示,算法的结束将是在\(\theta_{n\times 1}\)下降到无法继续下降为止。
其中,梯度方向由\(J(\theta)\)对\(\theta\)的偏导数确定。用公式来表达就是:
其中\(\alpha\)称为学习率(learning rate),直观的意义是,在函数向极小值方向前进时每步所走的步长。太大一般会错过极小值,太小会导致迭代次数过多。
具体的梯度方向是(此处为了方便计算,假设只有一组数据):
上面式子中的\(j\)表示的是第\(j\)个特征。从这个推导过程就可以知道,当初我们为什么要在公式前乘上\(\frac{1}{2}\)了。
这样,对于每一组训练数据,每一个特征分量\(\theta_j\)的变化是这样的(注意:此时括号中的符号改变了,因为是负梯度的方法向):
批梯度下降法(bath gradient descent)
在得到上面的公式之后,我们的算法也就形成了:
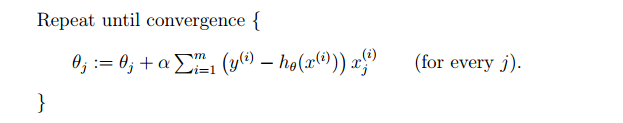
上述算法中的式子是针对所有的训练数据的,这是从公式\(\ref{1}\)变化而来,只是加入了一个累加的过程,此处不再证明。从公式中可以看到,每次迭代的时候,该算法都会遍历整个训练数据集,这个就被称为批梯度下降法(bath gradient descent)。需要注意的是,此处的梯度下降法是只能找到局部最优解,而非全局最优解。它有以下两个特点:
- 得到的结果是局部最优解,这依赖于初始值
- 每次迭代它的梯度大小都在变化,且越来越趋近于0
随机梯度下降法(stochastic gradient descent)
在利用批梯度下降法(bath gradient descent)进行计算的时候,你会发现,每计算一个参数分量,都需要遍历整个训练数据集,这样做的效率明显不高,因此我们有一个替代的算法:
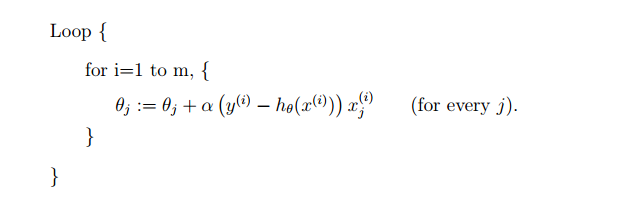
可以看到,这个算法每次都只利用了一组数据进行计算,这样就大大减少了计算量。这个算法称为随机梯度下降法(stochastic gradient descent)。但是,带来的相应后果就是,它最终得到的解可能是在真正的最小值的附近,而不是最小值本身。因此只有在数据量很大的情况下才会使用这个算法。
参考文献及推荐阅读
- 斯坦福《机器学习》公开课第二集及其配套讲义
- 机器学习中的数学
- 对线性回归,logistic回归和一般回归的认识
- 《统计学习方法》李航
Comments
So what do you think? Did I miss something? Is any part unclear? Leave your comments below