多元多项式判定问题(PIT)

在之前的学习笔记0 中，曾经分析过这个问题，但是，当时是对于单元多项式进行分析的，这要比多元的情况要简单得多。这次，我们将来看一下多元多项式的判定问题。

多元多项式判定问题可以表述成:

input: 定义在数域$F$上度为$d$的多元多项$P_1(x_1,x_2,\cdots,x_n),P_2(x_1,x_2,\cdots,x_n)$

output: 如果$P_1(x_1,x_2,\cdots,x_n) \equiv P_2(x_1,x_2,\cdots,x_n)$，则返回Yes，否则返回No

注意，在这里多元多项式的度是指每一项中所有变元的指数之和的最大值。

利用随机算法可以很巧妙地设计一种算法思路，首先令$Q(x_1,x_2,\cdots,x_n)=P_1(x_1,x_2,\cdots,x_n)-P_(x_1,x_2,\cdots,x_n)$，则原问题可以转化为判断$D(x_1,x_2,\cdots,x_n)\equiv 0$是否成立。

一个和学习笔记0中相似的算法可以用来进行判断:

Algorithms for PIT

从$F$中随机取出一个若干个数，形成集合$S$
从$S$中随机取出$r_1,r_2,\cdots,r_n$,形成向量$\vec{r}$
如果$D(r_1,r_2,\cdots,r_n)=0$,则返回Yes，否则返回No

现在我们要来分析这个算法的正确性。

我们的分析过程可以用归纳法:

首先，当$n=1$时，则多元多项式退化为单元多项式，根据在学习笔记0中的分析，使用该算法的情况下，单元多项式判断出错的概率是

$$ \begin{equation} Pr[D(r)=0] \leq \frac{d}{\vert S \vert} \end{equation} $$

我们假设在$n=k-1$时，$Pr[D(r_1,r_2,\cdots,r_{k-1})]\leq \frac{d}{\vert S \vert}$成立。

则当$n=k$时，可以$D(x_1,x_2,\cdots,x_n)$表示成:

$$ \begin{equation} D(x_1,x_2,\cdots,x_k) = \sum\limits_{i=0}^tx_1^iD_i(x_2,x_3,\cdots,x_k) \end{equation} $$

其中，$t$表示$x_1$的最大指数，这也就意味着，对于$D_t$来说，它的度最大是$d-t$,同时$D_t\not\equiv 0$

特别的，我们可以将$D$写成如下的特殊形式:

$$ \begin{equation} D(x_1,x_2,\cdots,x_k) = x_1^tD_t(x_2,x_3,\dots,x_k) + \bar{D}(x_1,x_2,\cdots,x_k) \end{equation} $$

注意，这里的$\bar{D}(x_1,x_2,\cdots,x_k)$中是不含$x_1^t$这一项的。

根据归纳法的证明步骤，在我们现在需要证明$Pr[D(r_1,r_2,\cdots,r_k)=0]\le \frac{d}{\vert S \vert}$

首先，令$\epsilon$表示事件"$D_t(r_2,r_3,\cdots,r_k)=0$"我们可以利用全概率法则，将$D(r_1,r_2,\cdots,r_k)$展开成:

$$ \begin{equation} Pr[D(\vec{r})=0] = Pr[D(\vec{r})=0\vert \epsilon]\cdot Pr[\epsilon] + Pr[D(\vec{r})=0\vert \neg\epsilon]\cdot Pr[\neg\epsilon] \label{ref0} \end{equation} $$

对于$D_t(x_2,x_3,\dots,x_k)$来说，它满足以下三点性质:

$D_t$来说，它有$k-1$个未知数，也即$k-1$个变元
$D_t$的度最大不会超过$d-t$
$D_t\not\equiv 0$

则根据我们之前的假设，应该有

$$ \begin{equation} Pr[D_t(r_2,r_3,\cdots,r_k)=0]\le \frac{d-t}{\vert S\vert}\label{ref1} \end{equation} $$

而当$D_t(r_2,r_3,\cdots,r_k)\neq 0$也即$\urcorner\epsilon$成立时，令

$$ \begin{equation} D(x_1,r_2,\cdots,r_k) = x_1^tD_t(r_2,r_3,\cdots,r_k) + \bar{D}(x_1,r_2,\cdots,r_k) = G(x_1) \end{equation} $$

则，$G$有如下三点性质:

$G(x_1)$是一个单元多项式
$G(x_1)\not\equiv 0$
$G(x_1)$的度为$t$(因为$D_t(r_2,r_3,\cdots,r_k)\neq 0$,所以$x_1^t$一定存在,同时$\bar{D}(x_1,r_2,\cdots,r_k)$中又不包含$x\_1^t$这一项)

所以有

$$ \begin{equation} Pr\big[D(\vec{r})=0\big\vert \neg\epsilon\big] = Pr[G(r_1)=0\big\vert \neg\epsilon]\leq \frac{t}{\vert S \vert}\label{ref2} \end{equation} $$

而根据$\ref{ref0}$的等式，我们可以做如下变换:

$$ \begin{equation} Pr\big[D(\vec{r})=0\big] = Pr\big[D(\vec{r})=0\big\vert \epsilon\big]\cdot Pr\big[\epsilon\big] + Pr\big[D(\vec{r})=0\big\vert \neq\epsilon\big]\cdot Pr\big[\neg\epsilon] \leq Pr[\epsilon] + Pr[D(\vec{r}=0)\vert \neg\epsilon] \end{equation} $$

而上式中右侧的$Pr[\epsilon]$和$Pr[D(\vec{r}=0)\vert \neg\epsilon]$可以通过$\ref{ref1}$和$\ref{ref2}$进行计算，因此我们就能得到:

$$ \begin{equation} Pr\big[D(\vec{r})=0\big]\le Pr[\epsilon] + Pr[D(\vec{r}=0)\vert \neg\epsilon] = \frac{d-t}{\vert S \vert} + \frac{t}{\vert S \vert} = \frac{d}{\vert S \vert} \end{equation} $$

$\Box$

综上，我们证明了当$P\_1,P\_2$为多元多项式时，该算法依然能保持$\frac{d}{\vert S \vert}$的概率返回错误解，利用独立重复运行的方法，可以将这个错误率进一步减小，因此这就证明了该算法的可行性。

最小割问题

现在我们来看另外一个问题——最小割问题，最小割问题的描述比较复杂,具体问题描述可以从wiki上找到，这里我就不多阐述了，直接来看一下解决这个问题的随机化的算法吧。

首先，我们需要定义一种"合并(contract)"操作，它将图中一条边上的两个定点合并，但是除了这两个点之间的边以外的边均保持不变(有可能因此会形成平行边)。

如下图所示，粗边被contract之后就得到右边的图了。

{% asset_img min-cut.png 最小割 %}

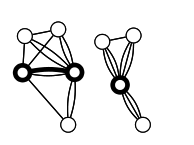
在定义了contract操作之后，我们就能够在图$G(V,E)$上构造我们随机化的算法了:

RandomContract(Karger 1993)

while $\vert V \vert > 2$ do: {

随机地从G中选出一条边$e$
对于$e$执行contract操作,G = contract(G,e)

} return E

算法最终返回的是只有两个点的图，而这两点中有着很多的平行边，而此时所有平行边的个数就是我们最小割中边的个数。

还是一样的，我们需要分析这个算法的正确性。

首先，我们需要引入两个引理:

引理1: 如果选取的$e$不存在于最小割$C$中，则contract(G,e)中的最小割大小不会超过$G$中的最小割大小。也即，contract操作不会破坏最小割。

证明: 因为最小割$C$将图分成两部分，假设分别是$P$和$Q$，则现在只有三种边，分别属于$C$,$P$和$Q$，而我们的前提条件是$e\not\in C$，所以$e$之能是属于$P$或$Q$，因此并不会改变原来的$C$.$\Box$

引理2: 如果$C$是$G(V,E)$中的最小割，则$\vert E\vert \ge \frac{\vert V\vert\vert C\vert}{2}$

证明: 因为$C$是$G(V,E)$中的一个最小割，则说明$G$中所有的点的度都至少为$C$，则边集的大小至少为$\frac{\vert V\vert\vert C\vert}{2}$，也即$\vert E\vert \ge \frac{\vert V\vert\vert C\vert}{2}$ $\Box$

有了这两个引理，我们可以开始对Karger算法进行分析了。

很显然，要该算法返回正确的结果，就必须保证每次随机选择的边$e$均不能属于$C$，因为一旦$C$中的边contract了，则最小割就被破坏了，算法会返回出一个错误的结果。

考虑单次随机选择的情况，假设前面的$i-1$次随机选择都没有选取到$C$中的边，则第$i$次依然没有选取$C$中的边的概率为:

$$ \begin{equation} Pr[e\not\in C] = 1 - \frac{\vert C\vert}{\vert E_{i} \vert} \end{equation} $$

其中$E\_{i}$表示经过$i-1$次选取之后，图中剩余的边集。

而根据引理2，我们可以得到:

$$ \begin{equation} Pr[e\not\in C] = 1 - \frac{\vert C\vert}{\vert E_{i} \vert} \ge 1 - \frac{2}{\vert V_i \vert} \end{equation} $$

其中$V_{i}$表示经过$i-1$次选取之后，图中剩余的点集。而又因为，每一次的contract操作都会减少一个点，因此$V_i = n-i+1$

令$\epsilon$表示事件"在$n-2$次选择中，都没有选中$C$中的边"

因此在整个算法过程中，$C$中没有边被选中的概率为:

$$ \begin{aligned} Pr[\epsilon] &= \prod\limits_{i=1}^{n-2}Pr[第i次选择没有选中C中的边\vert 前i-1次选择都没有选中C中的边] \\ &\ge \prod\limits_{i=1}^{n-2}\bigg( 1 - \frac{2}{\vert V_{i} \vert} \bigg) \\ &= \prod\limits_{i=1}^{n-2}\bigg(1- \frac{2}{n-i+1} \bigg) \\ &= \prod\limits_{k=3}^{n}\frac{k-2}{k} \\ &= \frac{2}{n(n-1)} \end{aligned} $$

这就说明，每一次运行该算法，能够以$\frac{n(n-1)}{2}$的概率得到正确的结果，因此，如果我们独立重复执行该算法$n(n-1)$次，然后最终返回一个最小的$C$，则返回一个正确解的概率是:

$$ \begin{equation} Pr[得到正确解] = 1-Pr[每一次运行都失败] \ge 1-\bigg( 1- \frac{2}{n(n-1)} \bigg)^{\frac{n(n-1)}{2}} \ge 1-\frac{1}{e} \end{equation} $$

这个结果很好，因为它是一个和$n$无关的常量！

Flyaway is the owner of this blog.

So what do you think? Did I miss something? Is any part unclear? Leave your comments below

Comments

随机算法学习笔记1-PITandMin-Cut

多元多项式判定问题(PIT)

最小割问题

Comments

Published

Category

Tags

Contact