之前的两篇文章记录梯度下降法的原理 及其矩阵形式的Normal Equations ,这次用代码实现起来,以便加深理解。代码中使用的具体数据来源于斯坦福公开课网站。
写在前面
通常进行科学计算的时候,首选工具一般都是matlab,但是我觉得matlab太过臃肿,而且matlab本身作为一种编程语言,在矩阵计算以外有着很多不便的地方,因此果断放弃matlab,转而投向Python的伟大怀抱。网上流传着这样一个等式:numpy+scipy+matplotlib = matlab,其中numpy、scipy和matplotlib都是开源的Python库,将这几个库组合起来,就能完全取代matlab,并且本身具有良好的可扩展性(Python世界中有着无数的优秀开源软件包)。更多详细资料,可以参考这里。
代码
关于梯度下降法的具体Python代码如下:
#!python
import numpy as np
import matplotlib.pyplot as plt
def H(theta,x):
return theta.dot(x)
def Read():
x = np.loadtxt('ex3x.dat')
y = np.loadtxt('ex3y.dat')
m = len(x)
t = np.ones((m,1))
x = np.concatenate((t,x),axis=1)
return (x,y,m)
#gradient的计算
def cal(alpha,theta,x,y,m):
n = x.shape[1]
newtheta = np.array([0]*n,dtype=np.float)
for j in range(0,n):
count = 0
for i in range(m):
count += (H(theta,x[i,:]) - y[i]) * x[i,j]
newtheta[j] = (theta[j] - alpha / m * count )
return newtheta
#Cost Function
def J(theta,x,y,m):
return np.transpose(x.dot(theta)-y).dot(x.dot(theta)-y)/(2*m)
#Normal Equation
def normalequation(x,y):
return np.linalg.inv(np.transpose(x).dot(x)).dot(np.transpose(x)).dot(y)
#根据不同的alpha值,画出图像
def gradent_descent():
(x,y,m) = Read()
sigma = np.std(x,0)
mu = np.mean(x,0)
#数据归一化
x[:,1] = (x[:,1]-mu[1]) / sigma[1]
x[:,2] = (x[:,2]-mu[2]) / sigma[2]
n = x.shape[1]
theta = np.array([0]*n,dtype=np.float)
j = []
alpha=0.01
for i in range(50):
j.append(J(theta,x,y,m))
theta = cal(alpha,theta,x,y,m)
plt.plot(range(50),j,'b-',label=r'$\alpha = 0.01$')
j = []
theta = np.array([0]*n,dtype=np.float)
alpha=0.03
for i in range(50):
j.append(J(theta,x,y,m))
theta = cal(alpha,theta,x,y,m)
plt.plot(range(50),j,'r-',label=r'$\alpha = 0.03$')
j = []
theta = np.array([0]*n,dtype=np.float)
alpha=0.1
for i in range(50):
j.append(J(theta,x,y,m))
theta = cal(alpha,theta,x,y,m)
plt.plot(range(50),j,'y-',label=r'$\alpha = 0.1$')
j = []
theta = np.array([0]*n,dtype=np.float)
alpha=0.3
for i in range(50):
j.append(J(theta,x,y,m))
theta = cal(alpha,theta,x,y,m)
plt.plot(range(50),j,'b--',label=r'$\alpha = 0.3$')
j = []
theta = np.array([0]*n,dtype=np.float)
alpha=1
for i in range(50):
j.append(J(theta,x,y,m))
theta = cal(alpha,theta,x,y,m)
plt.plot(range(50),j,'r--',label=r'$\alpha = 1$')
j = []
theta = np.array([0]*n,dtype=np.float)
alpha=1.3
for i in range(50):
j.append(J(theta,x,y,m))
theta = cal(alpha,theta,x,y,m)
plt.plot(range(50),j,'y--',label=r'$\alpha = 1.3$')
plt.xlabel('Number of interations')
plt.ylabel('Cost J')
plt.legend()
plt.show()
if __name__=='__main__':
#画出图像
gradent_descent()
(x,y,m) = Read()
#利用normal equation计算theta值
theta = (normalequation(x,y))
#预测未知数据
print('predict:',end=' ')
print(H(theta,np.array([1,1650,3])))
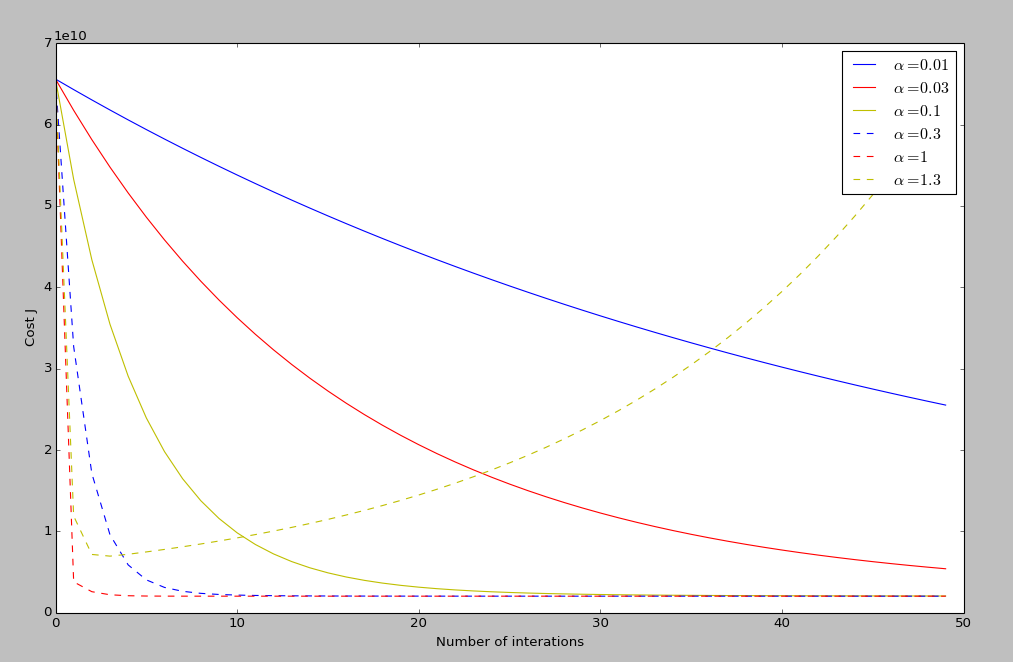
运行结果
Comments
So what do you think? Did I miss something? Is any part unclear? Leave your comments below
comments powered by Disqus