最近在阅读论文过程中，发现我们常常需要估计一个大集合中的某个子集的大小，而这两个集合都是非常巨大的，遍历一遍非常耗时，在实际过程中根本不可行。因此，我们需要一种方式能够快速估计子集的大小。一个典型的应用场景就是在Ranking Problem中，我们需要知道排在当前实例$x$之前有多少个元素。而且这样的操作我们需要对每个实例都进行，很显然每次都遍历整个集合是不现实的。

Sampling

一个合理方法就是通过采样来估计集合大小。

首先，我们假设大集合是$Y$,它的大小$\vert Y\vert$是已知的，我们需要估计的子集是$S\subset Y$，而$\vert S\vert$是未知的，也是需要我们估计的。

几何分布

在论文WSABIE: Scaling Up To Large Vocabulary Image Annotation中提到了一种利用几何分布的采样方式。具体过程是:

不停地从$Y$中随机挑选(有放回)一个元素$y$，直到采样出的元素$y\in S$为止。记录下一共的采样次数，记为$N$. 那么，$S$的大小就可以估计为$\vert S\vert =\frac{\vert Y\vert}{E[N]}\approx \frac{\vert Y\vert}{N}$.

证明:

整个过程是非常简单的，其证明过程也同样简单。我们用$p$来表示采样出的元素$y$属于$S$的概率，那么很显然我们有:

$$ p = Pr[y\in S] = \frac{\vert S\vert}{\vert Y\vert} $$

那么，根据采样的方式，我们继续得到:

$$ Pr[N=i] = (1-p)^{i-1}p $$

因为，当$N=i$时，表示我们采样了$i$次，说明前$i-1$都没有采样到$S$中的元素，第$i$次采样到了$S$中的元素。这是一个几何分布，那么它的期望¹就是:

$$ E[N] = \frac{1}{p} = \frac{\vert Y\vert }{\vert S\vert} $$

讲上述公式转化一下，我们就能得到:

$$ \vert S\vert = \frac{\vert Y\vert}{E[N]} $$

同时，我们知道，当采样轮数趋近于无穷大时，经验值就等于期望值，因此我们有:

$$ E[N] = \lim\limits_{m\rightarrow \infty}\frac{1}{m}\sum\limits_{i=1}^m N_i. $$

其中，$N_i$表示第$i$轮采样中，需要的采样次数。为了快速估计，我们可以使$m=1$，此时，我们就能得到:

$$ \vert S\vert \approx \frac{\vert Y\vert}{N} $$

$\blacksquare$

贝努利分布

除了上述基于几何分布的采样方式以外，实际上还有其他的采样方式。我们可以采用基于贝努利分布的采样方法。其具体过程如下:

持续地从$Y$中连续(有放回)采样$N$次，检查这$N$个元素中有多少是属于$S$的，记为$M$。显然，$M<N$. 那么，$\vert S\vert$的大小可以估计为$\vert S\vert=\frac{E[M]\cdot \vert Y\vert}{N}\approx \frac{M\vert Y\vert}{N}$.

证明:

同样的，我们首先用$p$表示任意一个元素$y\in Y$属于$S$的概率，我们有:

$$ p=Pr[y\in S] = \frac{\vert S\vert}{\vert Y\vert} $$

那么，根据这种采样方式，我们有:

$$ Pr[M=i]=\binom{N}{i} (1-p)^{N-i} p^i $$

这表示$N$次采样中有$i$次采样到了$S$中的元素，而每次采样都是有放回且独立的。这是一个贝努利分布，那么它的期望²是:

$$ E[M]=pN=\frac{\vert S\vert}{\vert Y\vert}\cdot N $$

将上述公式重写，我们可以得到:

$$ \vert S\vert = \frac{E[M]}{N} \cdot \vert Y\vert $$

同样根据期望值的定义，我们有:

$$ E[M] = \lim\limits_{m\rightarrow \infty}\frac{1}{m}\sum\limits_{i=1}^m M_i $$

其中$M_i$表示第$i$轮采样中，有多少个元素是属于$S$的。同样，为了快速估计，我们可以使$m=1$，我们即可得到:

$$ \vert S\vert \approx \frac{M\vert Y\vert}{N} $$

$\blacksquare$

实验

为了比较这两种不同采样方式的差别，我做了一些实验。下面是我的实验结果。

估计值的准确性

首先我比较了这两种采样方式得出的估计值的准确性，在不同的$\vert Y\vert, \vert S\vert$的比例情况下，我们得到如下四张图:

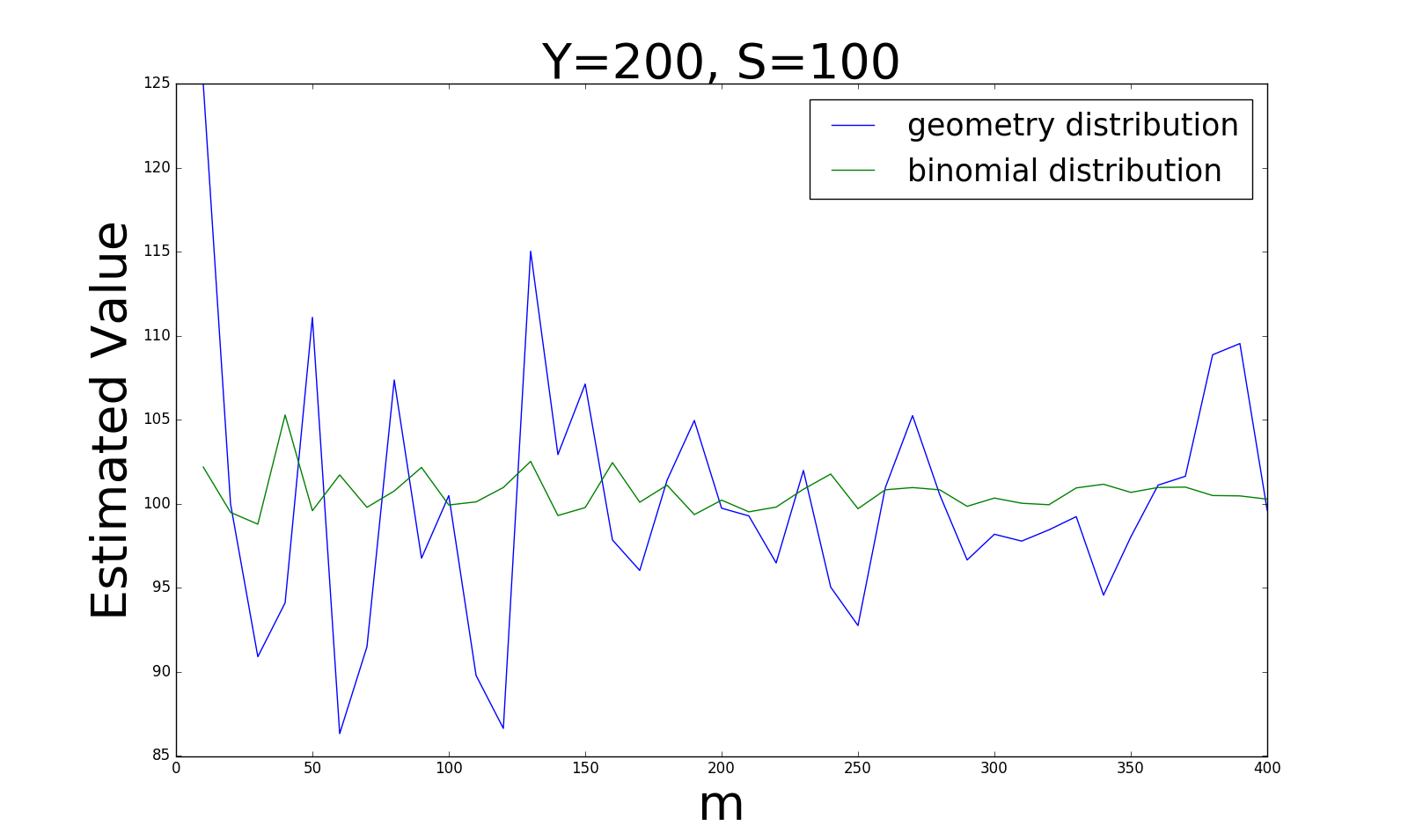
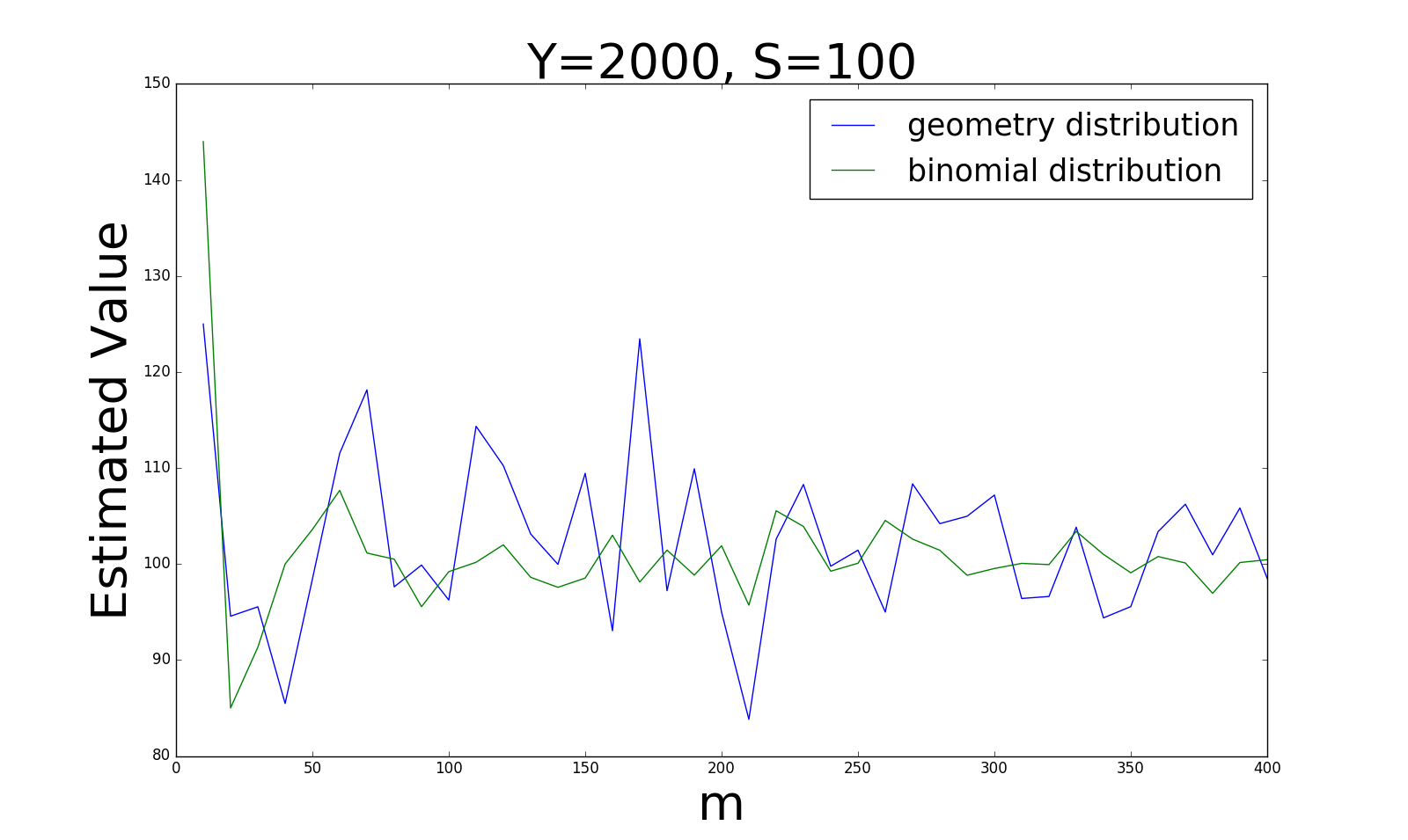
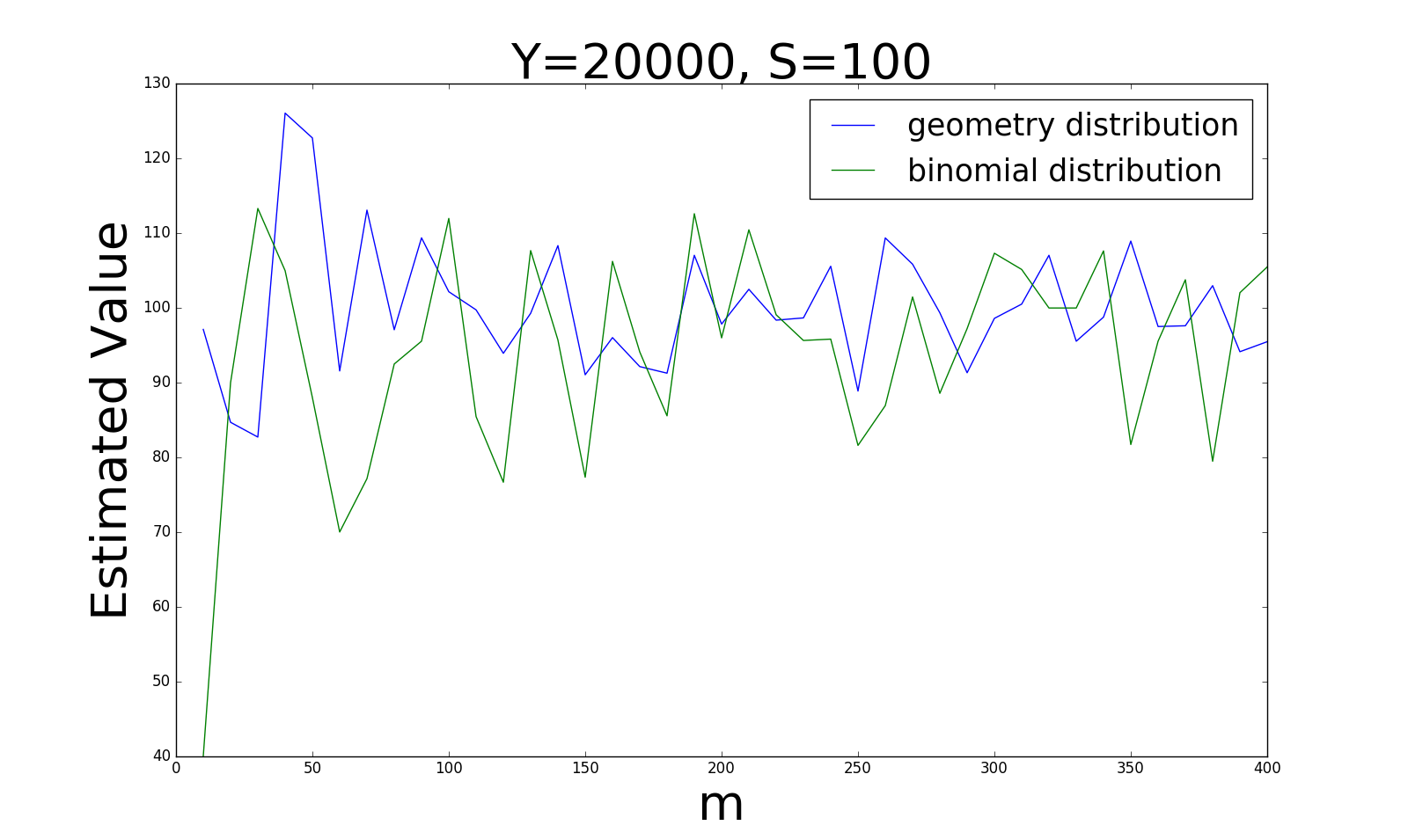
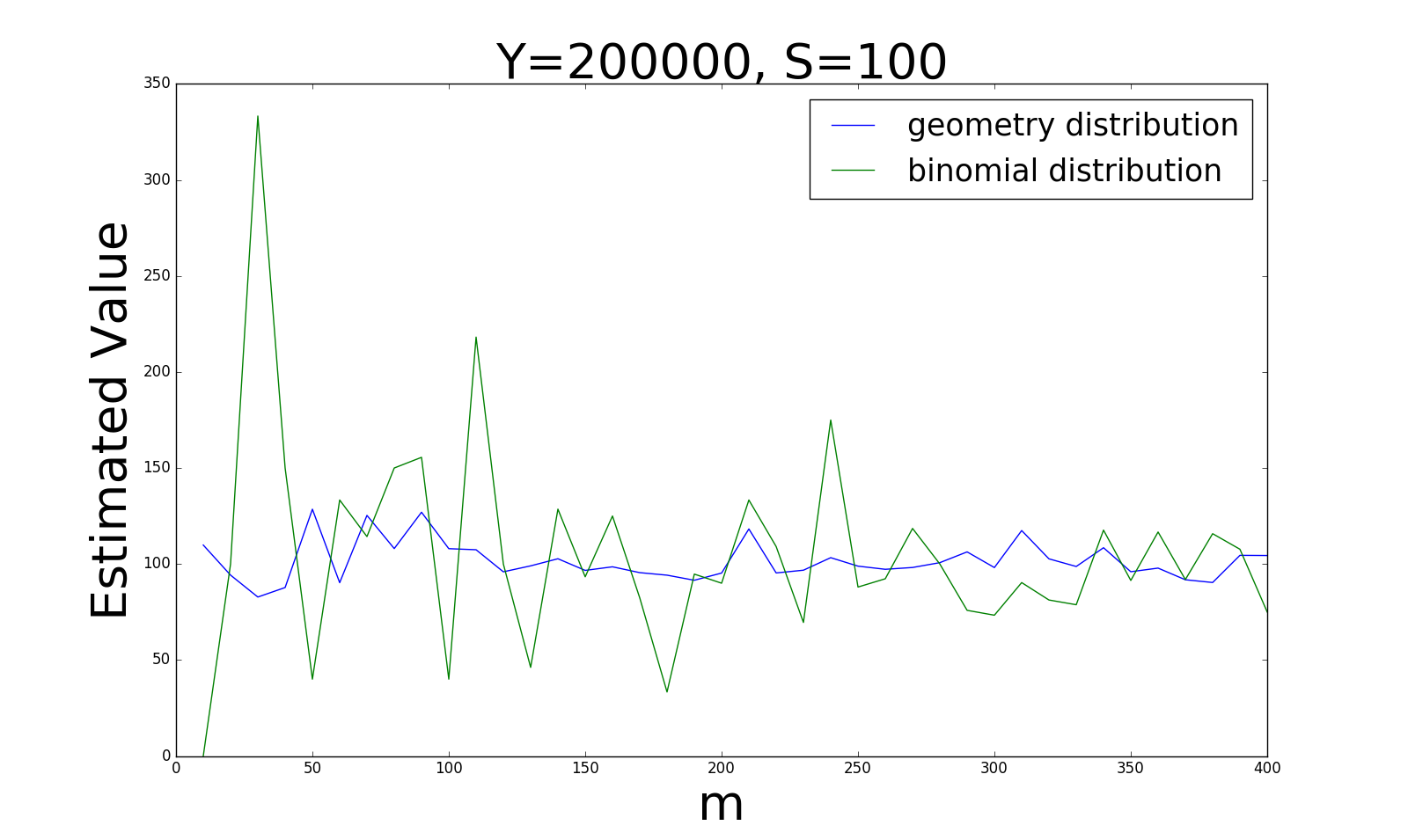
Experiments

从四张图的变化趋势，我们可以得出以下结论：

当$\vert Y\vert$和$\vert S\vert$比例较大(0.5)时，贝努利分布的采样方式更稳定；而当比例逐渐变小时(0.0005), 几何分布的估计值更加稳定。

采样时间花费

另外一个重要指标是采样的时间，毕竟，我们一切的工作都是希望能加速计算过程。下面四张图是在同样的设定下，采样时间的对比:

{% asset_img timeY200S100.png %} {% asset_img timeY2000S100.png %} {% asset_img timeY20000S100.png %} {% asset_img timeY200000S100.png %}

Time Time Time Time

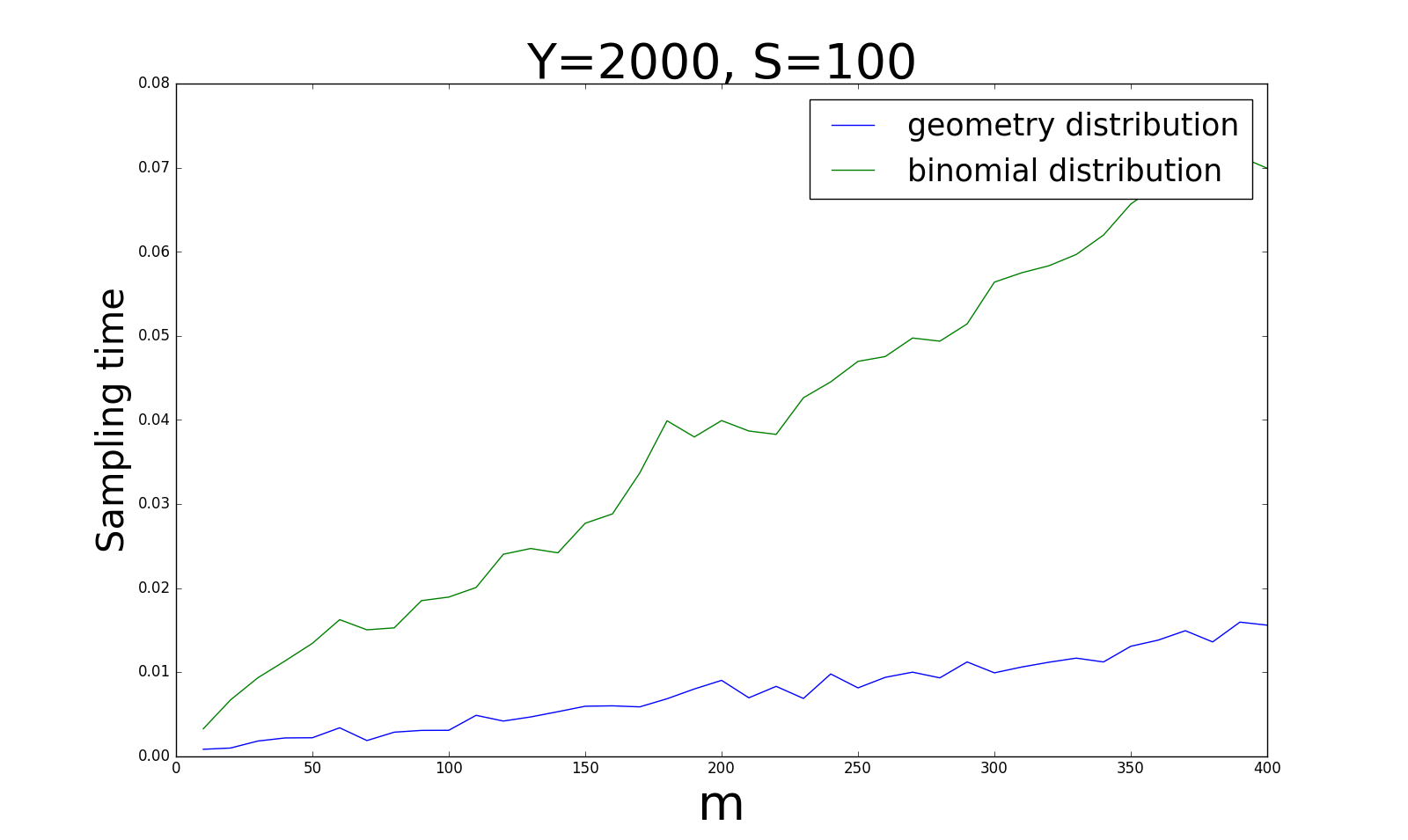
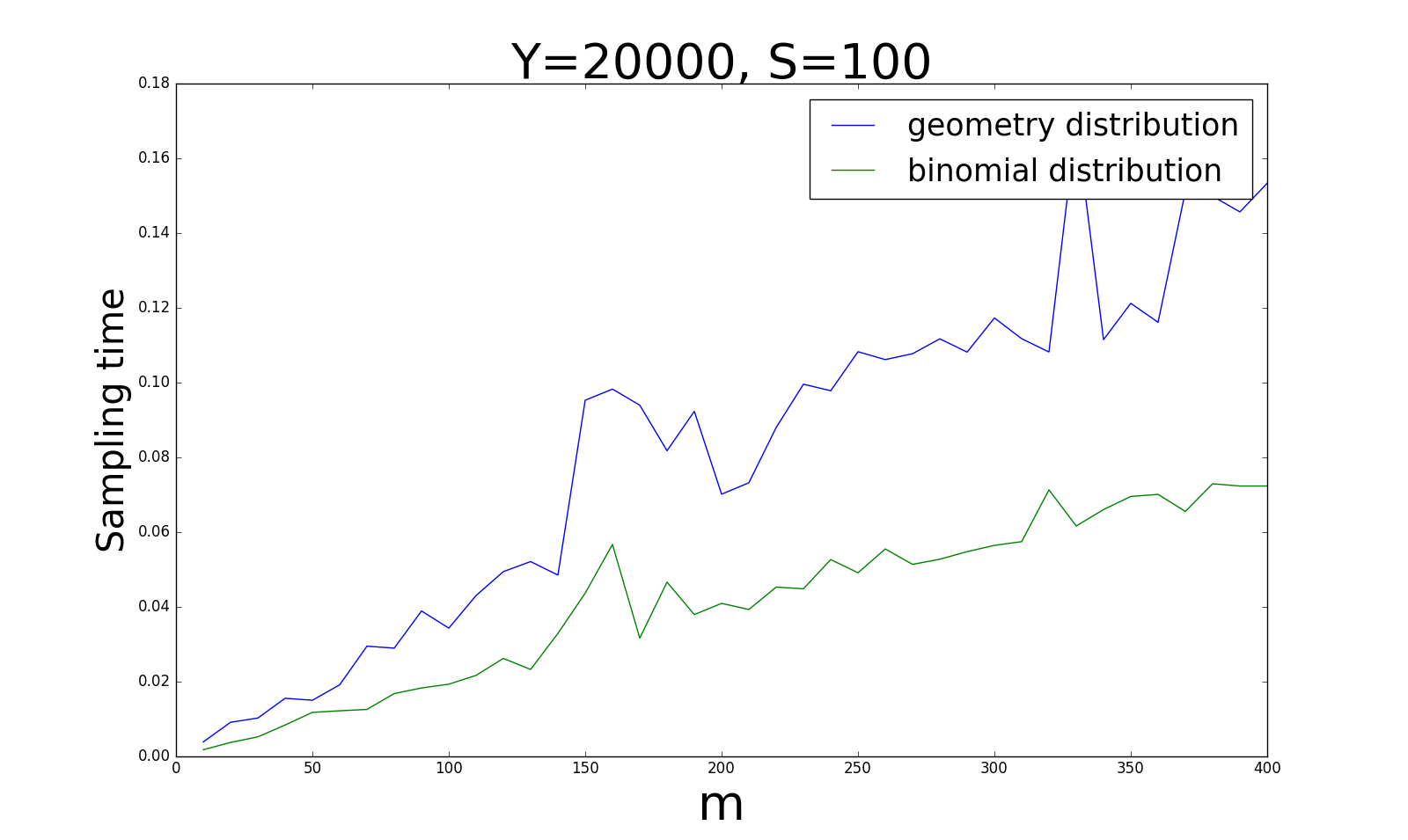
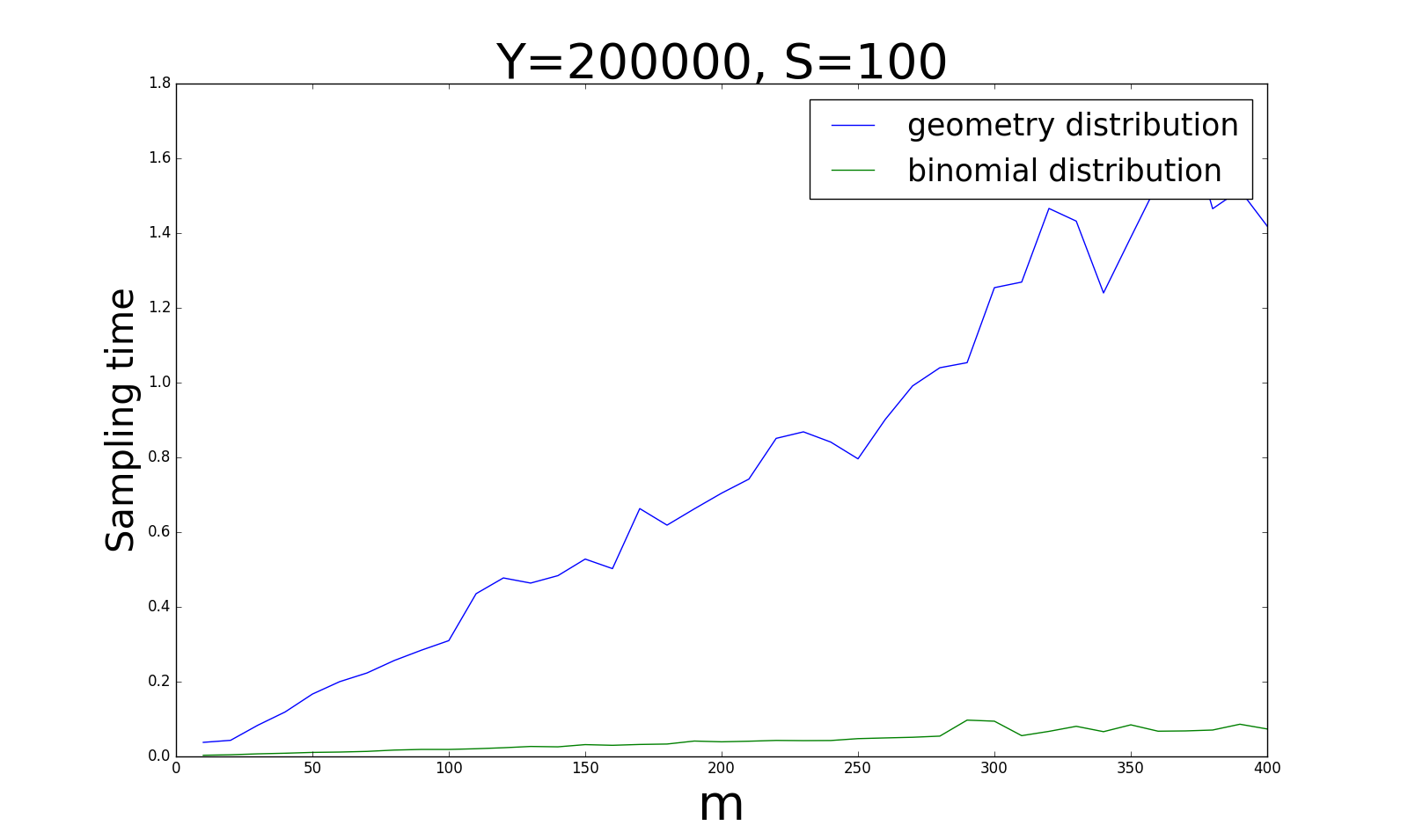
对于时间花费来说，当$\vert Y\vert$和$\vert S\vert$比例较大(0.5)时,几何分布要明显比贝努利分布快；而当比例逐渐变小时(0.0005)，几何分布将会花费越来越多的时间，此时贝努利分布就更占优势。

参考资料

更新日志

2017年2月18日完成初稿
2017年2月19日添加实验结果并发布

关于几何分布的期望证明，我在这篇博文中证明过。 ↩
关于贝努利分布的期望证明，我在这篇博文中证明过。 ↩

Flyaway is the owner of this blog.

So what do you think? Did I miss something? Is any part unclear? Leave your comments below

Comments

Sampling Trick

Sampling

几何分布

贝努利分布

实验

估计值的准确性

采样时间花费

参考资料

更新日志

Comments

Published

Category

Tags

Contact